Welcome to AE Resources

Converted document PRODUCTS OF INERTIA EXAMPLES

PRODUCTS OF INERTIA EXAMPLES

Find the product of inertia I_xy for the prism shown in the figure below. The prism is homogeneous and has a density of ρ and a mass m = ρV.

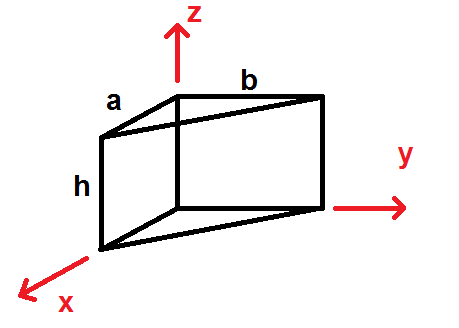
Answer: I_xy = (mb)/(12a)(6a² − 8ab + 3b²)

Solution: To solve this problem, begin with the definition of the product of inertia, I_xy in Cartesian coordinates:

(1) I_xy = ⌠⌡_VρxydV

Since the material of the prism is homogeneous, ρ can be moved outside of the integrals. One way to define the integral limits is to find the integral from z=0 to z=h, and sweeping from y=0 to y=b. As y sweeps from 0 to b, the value of x sweeps from x = 0 to x= a-y as seen in the figure below.

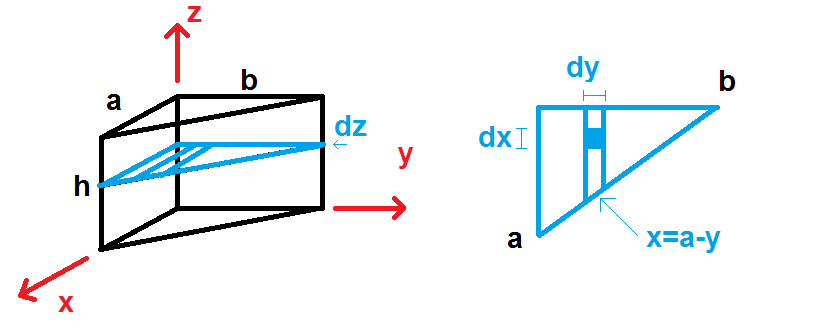
Thus, the product of inertia can be solved as:

(2) I_xy = ρ^h⌠⌡₀^b⌠⌡₀^a − y⌠⌡₀xydxdydz = ρ^h⌠⌡₀^b⌠⌡₀(1)/(2)(a − y)²ydydz = ρ^h⌠⌡₀^b⌠⌡₀(1)/(2)(a²y − 2ay² + y³)dydz = ρ^h⌠⌡₀(1)/(2)(a²b² ⁄ 2 − 2ab³ ⁄ 3 + b⁴ ⁄ 4)dz = (ρ)/(2)h⎛⎝(a²b²)/(2) − (2ab³)/(3) + (b⁴)/(4)⎞⎠ = (ρ)/(2)b²h⎛⎝(a²)/(2) − (2ab)/(3) + (b²)/(4)⎞⎠ = (ρ)/(2)b²h⎛⎝(6a²)/(12) − (8ab)/(12) + (3b²)/(12)⎞⎠

The volume of the prism can be defined as V = 1 ⁄ 2abh. Since m = ρV, the final answer in terms of mass is: I_xy = (mb)/(12a)(6a² − 8ab + 3b²)