PRODUCTS OF INERTIA

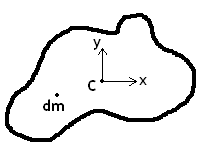
Products of inertia are inertia properties that result from moment contributions in a direction not along the axes of the reference frame used. The definition of the products of inertia for a three-dimensional body, as seen in Figure 1↑, in Cartesian coordinates with the origin of the axes located at point C, is as follows:

where dm denotes elemental mass. Physically, the products of inertia are the products of the perpendicular distances from the respective axes referred to the subscript for each incremental mass dm over the entire body. For instance, I^C_xy represents the product of the x coordinate and the y coordinate that describe the elemental mass dm, integrated over the entire body.

Notice that these values here are negative. Some sources include this negative sign in the definition of the products of inertia as shown here, while others write the products of inertia as negative values in the inertia matrix. Either way is acceptable as long as one is aware of which convention is being used and remains consistent in its use.

To make calculations easier, the inertia matrix can be simplified to a diagonal matrix by taking advantage of symmetry. If z is the axis of symmetry, the products of inertia disappear. If the plane formed by the x and y axes is the plane of symmetry, the products of inertia I_xz and I_yz disappear. The products of inertia indicate rotational motion that is not purely about the axes. Moments of inertia refer to the rotation about each axis.