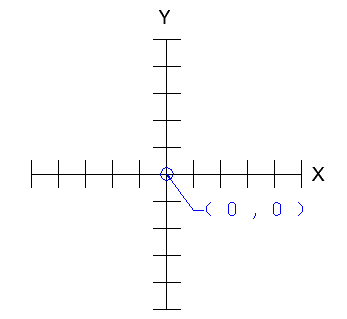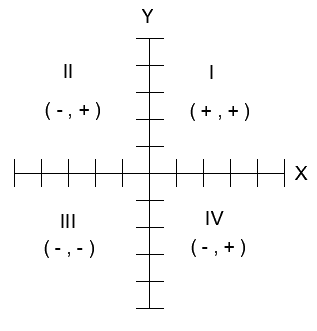CARTESIAN COORDINATE SYSTEM

Also referred to as the rectangular coordinate system, this useful coordinate system has been a primary coordinate system since the 17th century. Invented by René Descartes, the Cartesian coordinate system revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Since it is named after a specific person, “Cartesian” is capitalized. Another name for a coordinate system is "reference frame" or "frame of reference".

A Cartesian coordinate system specifies a point in space by a set of numerical coordinates that are fixed in an orthogonal reference frame, which is defined in each direction (one, two or three) by lines known as “axes”. The point of intersection where these axes meet or originate is referred to as the “origin”. This is illustrated for a two dimensional coordinate space (a planar system) in Fig. 1↑, where it has the corresponding coordinates (0, 0).

The coordinate system can be defined as a finite system where the axes end (as in Fig. 1↑) or an infinite system (as in Fig. 2↓).

In one dimension, the Cartesian coordinate system specifies a point on a line by a single numerical coordinate that is fixed in a reference frame, which is defined in a single direction or axis, typically defined (but not always) as the x axis. A one-dimensional Cartesian reference frame is shown in Fig. 2↑.

In a conventional two-dimensional (2-D) Cartesian coordinate system, the horizontal axis is typically defined as the x axis and the vertical axis as the y axis; however, this may not always the case. For this reason, the axes should always be labeled to avoid confusion.

A Cartesian coordinate system specifies a point on a plane by a pair of numerical coordinates that are fixed in an orthogonal reference frame, which is defined in each direction (one, two or three) by lines known as “axes”. The point of intersection where these axes meet is referred to as the “origin” and, in two dimensions, it has the corresponding coordinates (0, 0), as illustrated in Fig.  1↑. The first zero represents the x value and the second zero represents the y value as (x, y).

In the 2-D system, there are two axes that divide the plane into four quadrants denoted by Roman numbers as shown in Fig. 3↑. In the first quadrant both the x and the y components are positive. In conventional (but not all) applications, positive values are defined to the right of the origin for the x values and above the origin for the y values. This is the reason why quadrant III is negative for both x and y values.