VECTOR MATHEMATICS

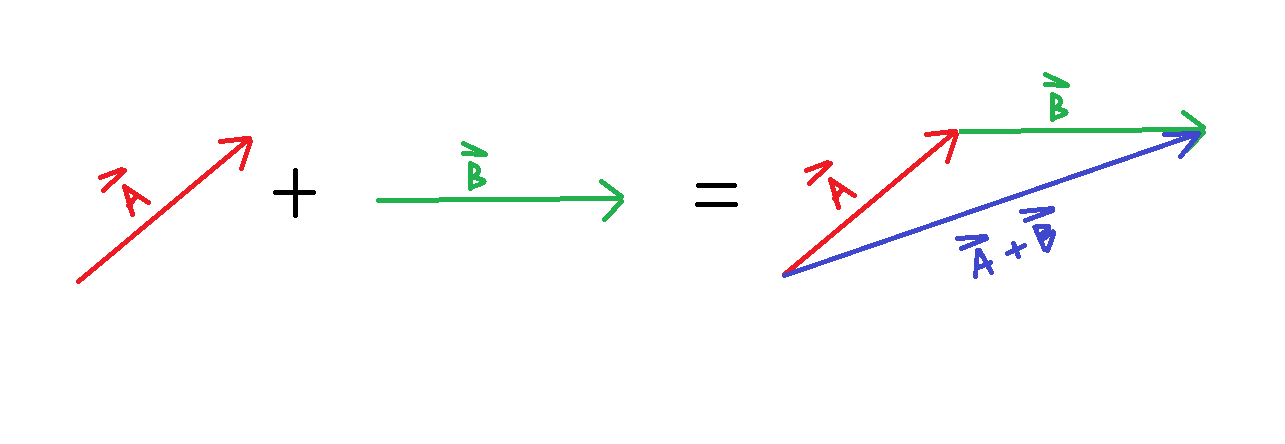
Addition of two or more vectors is an important concept to understand in engineering, in particular dynamics. The first step in the process is to define the vectors, both in magnitude and direction. Given vectors A =  < 10, 5, 0 >  and B =  < 10, 0, 0 > , the process begins by drawing a graphical representation of the two vectors. Once the first step has been completed, the two vectors can be added by orienting the tail (portion of the vector without the arrow) of B right on top of the arrow or head of vector A. Next, a new vector can be drawn that starts at the tail of A and ends at the head of B as shown in Fig. 1↓. This third vector represents the addition of A and B, thus, it is denoted as A + B =  < 10, 5, 0 >  +  < 10, 0, 0 >  =  < 20, 5, 0 > . The values of the new vector are the sum of each individual component of the two original vectors. A vector is denoted either by bold font or with an arrow over the vector name. In this section, bold font is used to identify the vector while the figures use the arrow.

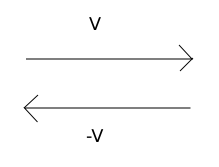
One important concept about vector addition that is sometimes confusing is vector subtraction, which can be approached as vector addition with negative numbers. For example, how does one add A + ( − B)? The sign change indicates a change in direction of the vector, so that the vector B that initially pointed to the right, now points to the left, as illustrated in Fig. 2↓

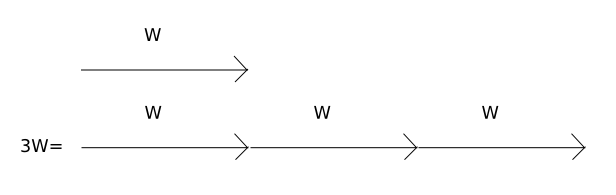
Scalar multiplication of vectors is yet another important concept. A scalar number that multiplies a vector will simply have every component multiplied by the scalar: A =  < 10, 5, 0 > , then 3 A is  < 30, 15, 0 >  The scalar increases the vector length A by three as shown in Fig. 3↓.

For illustration purposes, the vectors shown in the examples are two dimensional. Three-dimensional vector mathematics follow the same rules as the two-dimensional vectors.