INTERPOLATION

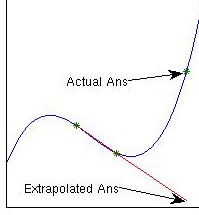
These examples also serve to illustrate that with more complex functions, the use of 1^st order interpolation is not advisable. Instead, the polynomials can be used as interpolators. These polynomials can also be used to extrapolate data, but these can be problematic, as is shown in Fig. 4↓.

A more mathematically (computationally) efficient polynomial uses the nested forms of the polynomial. These forms include the Newton and Lagrangian forms of the equations.

Consider the equation

Newton’s polynomial can be used for interpolating to fit a n^th polynomial to n+1 points. Here, x is the point of interest and at each point x_o, x₁, ..., x_n, the function p is known. In order to compute the unknown value, x, the coefficients b_o, b₁, ..., b_n must be computed. These are found using the following set of equations:

As an example to illustrate computation of the b coefficients, consider the situation when n = 2 This method uses the coefficients coefficients for lower n values for each successive larger n value. A two-dimensional array can be set up to compute the b(0:n) coefficients to use the function divided differences already computed. Similar to a Taylor series, a remainder or truncation error can be computed: Notice that the remainder calculation requires that the function be known. An alternate way to estimate the error when the function is not known is to use an additional known point for the error estimate: