Welcome to AE Resources
Converted document INTERPOLATION

INTERPOLATION

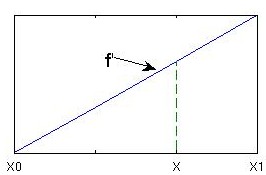
Interpolation is the calculation of the value of a function between the values already known (Fig. 1↓). The most common type of interpolation is linear (1st order) interpolation. This can be viewed as comparing similar triangles using a 1 st order Taylor series definition of the slope:
figure images/1st_order_slope.jpg
Figure 1 Illustration of the interpolation of a line.
f’  =  (f(x1) − f(xo))/(x1 − xo)       f’  =  (f(x) − f(xo))/(x − xo)
Setting the slopes equal:
(f(x1) − f(xo))/(x1 − xo) = (f(x) − f(xo))/(x − xo)   f(x) = f(xo) + ((x − xo))/((x1 − xo))[f(x1) − f(xo)]
This same process can be used with higher-order Taylor series to interpolate with comparably higher-order accuracies, but this can be complicated and not cost effective.
Higher-Order Interpolation
Instead for higher-order interpolation, different series approaches can be taken. A polynomial in power form (Eq. 1) can be written easily in its summation form (Eq. 2), as illustrated in Figs. 2↓ and 3↓ for polynomials about 0 and a value, c, respectively:
figure images/poly1.jpg
Figure 2 Polynomial interpolation.
(1) p(x)  =  ao + a1*x + a2*x2 + ... + anxn        =  n⎲⎳i = 0anxn
(2) p(x)  =  bo + b1(x − c)1 + ... + bn(x − c)n        =  n⎲⎳i = 0bn(x − c)n
figure images/poly2.jpg
Figure 3 A second polynomial interpolation example .
Next Page →
Next Page →