Welcome to AE Resources
Converted document WORK EXAMPLES

WORK EXAMPLES

WORK FROM DISPLACED BOX
Calculate the work done by a 5 N force if a box has a final displacement of 10 meters. Note that the 5 N force is at an angle of 20 degrees with respect to the horizon. Assume gravity has an acceleration of 10(m)/(s2)
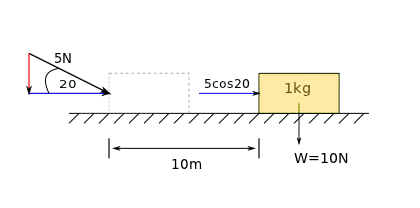
figure images/2.png
One should quickly realize that the only force acting in the direction of the displacement is the horizontal component of the 5 N force. Thus, one does not have to worry about the weight of the box or the vertical component of the 5 N force when calculating the work done since they are perpendicular to each other.
W = ∫F⋅ds
W = ∫1005cos(20)⋅ds
W = 4.7*s|100
W = [(4.7N*10m) − (4.7N*0m)]
W = 47N⋅m = 47Joules
WORK FROM VERTICAL DISPLACEMENT
Suppose there is a toy helicopter that is at rest on the ground. Find the work that this helicopter must do in order to reach an altitude of 10 meters. Assume the helicopters weight is 10 kg and gravity has an acceleration of 10(m)/(s2)
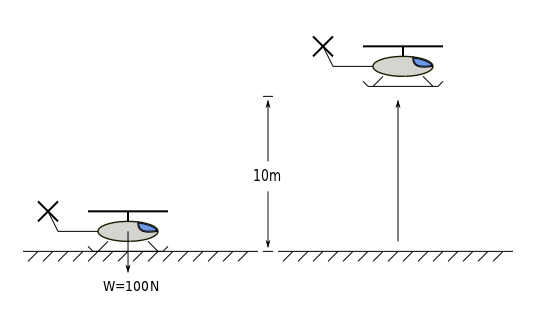
figure images/3.png
It is notable that this is a problem in which gravity does play a role since it is acting along the displacement axis.
W = ∫F⋅ds
W = ∫100 − 100N⋅ds
W =  − 100N|100
W = [( − 100N*10m) − ( − 100N*0m)]
W =  − 1000N⋅m =  − 1000 Joules
The negative sign simply means that the 1000 Joules must come from the helicopter. This means that in order to reach an altitude of ten meters, the helicopter must generate 1000 Joules.