Welcome to AE Resources

Converted document Converted document

THE SPHERICAL COORDINATE SYSTEM

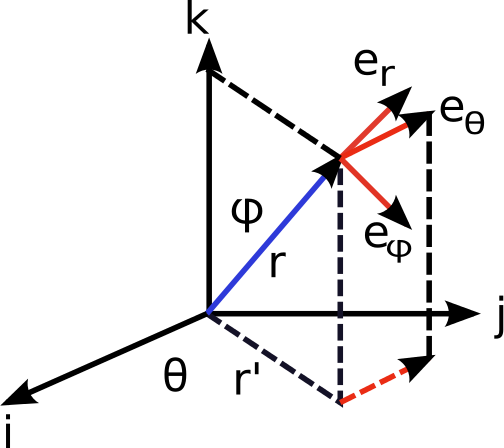
The spherical coordinate system is a curvilinear orthogonal coordinate system. Fig. 1↓ illustrates the spherical unit vectors, e_r, e_φ, and e_θ in the Cartesian frame (x, y, z).

Figure 1 The spherical coordinate system.

Fro the geometry, one can write spherical unit vectors as a function of i, j and k.

(1) e_r = sinφcosθi + sinφsinθj + cosφk

(2) e_φ = cosφcosθi + cosφsinθj − sinφk

(3) e_θ = − sinθi + cosθj

Since i, j and k are constant in time, the time derivatives of e_r, e_φ, and e_θ can be determined using eqs. 1↑ — 3↑:

(4) e_ṙ = φ̇cosφcosθi − θ̇sinφsinθi + φ̇cosφsinθj + θ̇sinφcosθj − φ̇sinφk

Regrouping all the underlined and double underlined terms in eq. 4↑ using eqs. 2↑ and 3↑, e_ṙ can be simplified to

(5) e_ṙ = φ̇e_φ + θ̇sinφe_θ

(6) e_φ̇ = − φ̇sinφcosθi − θ̇cosφsinθi − φ̇sinφsinθj − φ̇cosφk

Similarly e_φ̇ can be simplified from the underlined and double underlined terms in eq. 6↑, using eqns. 1↑ and 3↑:

(7) e_φ̇ = − φ̇e_r + θ̇cosφe_θ

(8) e_θ̇ = − θ̇cosθi − θ̇sinθj

Using the equality sin²α + cos²α = 1, the equation becomes

(9) e_θ̇ = − θ̇(sin²φ + cos²φ)cosθi − θ̇(sin²φ + cos²φ)sinθj

With eqs. 1↑ and 2↑, e_θ̇ simplifies to

(10) e_θ̇ = − θ̇(sinφe_r + cosφe_φ)

Calculating velocity and angular velocity in spherical coordinate is useful. Consider a point, P, whose position can be described as

(11) P = re_r