Welcome to AE Resources
INTEGRATION EXAMPLES

INTEGRATION EXAMPLES

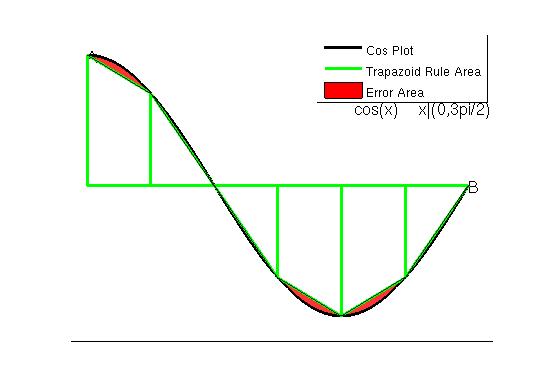
Trapezoidal Rule
The next easiest method is usually the trapezoidal rule. This method, as its name suggests, uses trapezoids formed between the two known points to estimate the integral. The error resulting from this method with an ’n’ of 6 is .0262 The error is much smaller than any of the methods shown so far:
figure images/cos_int_trapezoidal_rule.jpg
Figure 4 Trapezoidal Rule
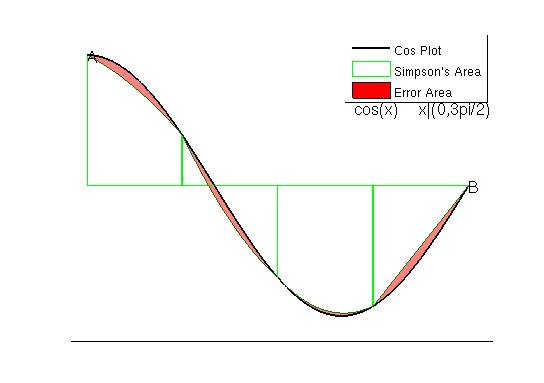
Simpson’s Rule
Simpson’s rule is by far the most accurate of the methods. In fact any polynomial with a power of 3 or less has an error of zero when calculated with Simpson’s rule. The method uses many small polynomials to create small parabolic sections that closely represent the curve. In order to be able to view the curves and how an error may result the ’n’ was reduced to 4. The result looks like:
figure images/cos_int_Simpsons_rule.jpg
Figure 5 Simpson’s Rule
A table which sums up all the methods and their errors:
Scheme Fscheme n Truncation Error Prediction Error
Left Hand Rule Fsch=-.5554 n=6 Etr=-.449 Epre=44.46%
Right Hand Rule Fsch=-1.3408 n=6 Etr=.3408 Epre=34.08%
Midpoint Rule Fsch=-1.0262 n=6 Etr=.0262 Epre=2.62%
Trapezoidal Rule Fsch=-.9481 n=6 Etr=-.0519 Epre=5.119%
Simpson’s Rule Fsch=1.00053 n=4 Etr=5.323 E − 4 Epre=0.053%
← Previous Page
← Previous Page