Welcome to AE Resources
Converted document INTEGRATION EXAMPLES

INTEGRATION EXAMPLES

This page compares the different methods of integration and their errors compared to continuous integration methods. For all the examples on this page the function f=cos(x) is used. The limits of integration are (0,(3π)/(2)) therefore:
(3π)/(2)⌠⌡0cos(x)dx =  − 1
In general all these methods will have smaller errors using more and smaller sections. The number of divisions is described by the variable ’n’. In the following examples large blocks (small n’s) are used so the error and how it results is clear.

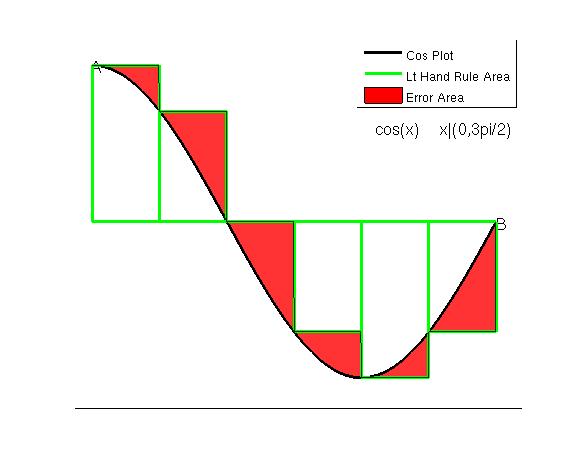
Rectangular or Midpoint Rule
The simplest method, which is also generally the most inaccurate, is the rectangular blocks to represent the sections of the graph.The error resulting from this method with an ’n’ of 6 is -.4446 and the result looks like:
figure images/cos_int_lt_hd_rule.jpg
Figure 1 Left Hand Rule
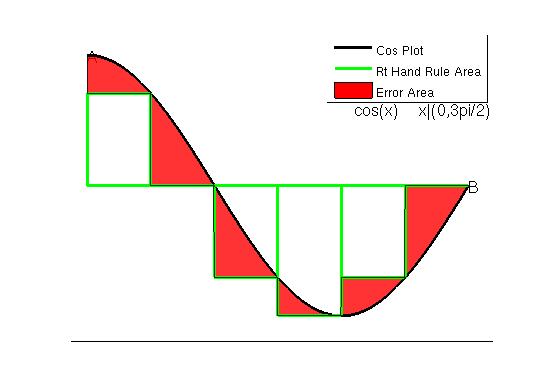
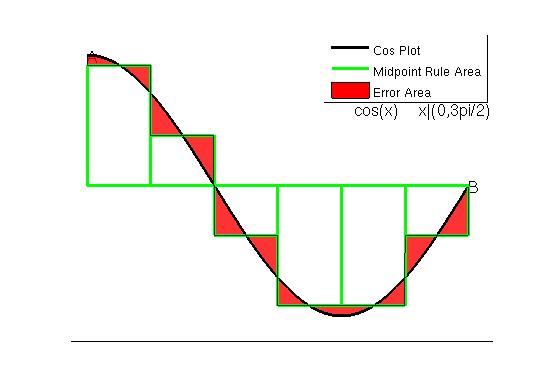
Rectangular methods can be computed at the right hand point of each section and the midpoint of each section. The error for right hand rule and midpoint rule with a ’n’ of 6 is .3408 and .0262 respectively, with results similar to
figure images/cos_int_Rt_hd_rule.jpg
Figure 2 Right Hand Rule

figure images/cos_int_midpoint_rule.jpg
Figure 3 Midpoint Rule

Next Page →
Next Page →