Welcome to AE Resources

Converted document Converted document

MOVING FRAMES OF REFERENCE

There are worked problems in the Examples section. The principles of moving reference frames are applied in a number of problems worked in other sections within the Dynamics section.

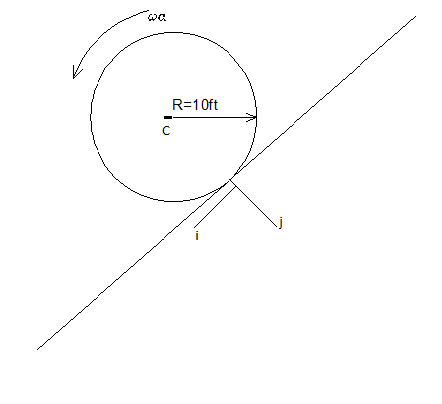
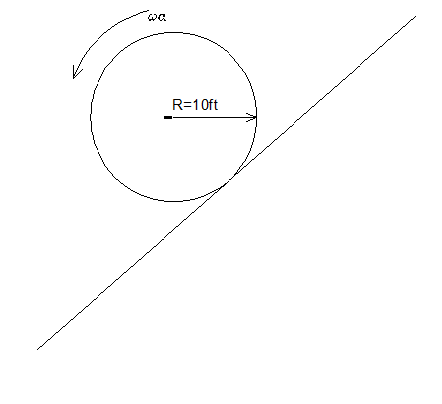
Example: Rolling cylinder

Consider the midplane of a homogeneous cylinder rolling down an incline. The radius of the cylinder is 10 feet. It has at the instant of the figure, an angular rotation of ω = 2(r)/(s) and an angular acceleration of α = 3(r)/(s²), both counterclockwise.

a) Find the point in the plane where there is zero acceleration.
b) Using only symbols and integration, compute the moment of inertia about the out of plane axis (z) axis at the point where the cylinder touches the inclined plane, if the density of the cylinder is ρ = ρ₀⎛⎝1 − (r)/(2R)⎞⎠ and the length of the cylinder is T.

figure images/Rolling_cylinder_quiz4_no_origin-1.png

Solution

a) This problem can be solved using the two-dimensional acceleration equation

a_Q = a_P + θ̈k × r_PQ − θ̇²r_PQ

. The \blfree body diagram of the figure, along with the coordinate system, is shown in Fig. 2↓.

figure images/Rolling_cylinder_quiz4.png

Figure 2 Free body diagram with coordinate system.

If the origin is set to O and substituting variables yields

a₀ = a_C + α × r_CO − ω²r_CO

a_C = α × r_IC = 3k × ( − 10j) = + 30i

Where C is the center of the cylinder, IC is the instantaneous center and r_CO is the unknown direction vector to location of zero acceleration:

0 = a_O = + 30i + 3k × r_CO − 4r_CO = + 30i + 3xj − 3yi − 4xi − 4yj

This equation can be decomposed into two equations, which can be solved simultaneously:

i: + 30 = 4x + 3y × 4 120 = 16x + 12y 3x − 4y = 0 j: 0 = 3x − 4y × 3 + 0 = 9x − 12y 3⎛⎝(24)/(5)⎞⎠ − 4y = 0 120 = 25x, x = (24)/(5) y = (18)/(5)