VELOCITY AND ACCELERATION IN MOVING FRAMES OF REFERENCE

Consider a point that is moving with respect to two frames of reference. For example, consider a plane in motion.

R moves downstream from F at some value (U_∞t, V_∞t, W_∞t), at a constant motion. Now, the plane may deviate from its course via maneuvers, gusts, etc. We reference these changes to the airplane itself, frame R. If we are calculating lift and drag, we need to reference these quantities to frame F. This means that we need to know the velocity and acceleration of the body in frame F.

We consider that the airplane is rigid for this analysis. Consider a point on the airplane's wingtip, P.

From kinematics, we know that:

We can differentiate this equation with respect to frame F as:

Since O is a fixed point in F, we can write,

. Since neither P or O' are defined in frame F, it cannot be differentiated with respect to frame F. So, we must use the derivative equation to transform it:

So that:

.

We have seen this equation before. If P is fixed in B (the airplane does not maneuver), the V_p/B=0 and all of the terms are defined in frame F.

In F:

In planar motion ω is a function of only one axis and r_o'p defined the distance in the plane described by the other two axes. This equation is also valid for our plane if the wings remain level; now the ω and r_o'p vectors are capable of being fully three dimensional. The common way of using this vector in aerodynamics and aeroelasticity is to define the equation as:

, where is the change of airplane center of gravity (c.g.) w.r.t. the fixed location. denotes how P changes w.r.t. the c.g.

Consider the following example problem. If we wish to find the velocity of point D on the disk w.r.t. the fixed frame of reference frame G.

ω_B/G = ω₂j, and V_D/B=V_Q/B+ω_A×r_QD
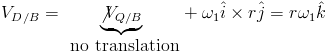
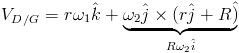